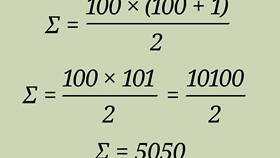В теории графов существует фундаментальное утверждение о сумме степеней вершин, которое имеет важные теоретические и практические применения.
Содержание
Основная теорема о сумме степеней
Для любого неориентированного графа сумма степеней всех его вершин равна удвоенному количеству рёбер:
| Формула | Σ deg(v) = 2E |
| Обозначения |
|
Доказательство теоремы
- Каждое ребро соединяет две вершины
- При подсчёте суммы степеней каждое ребро учитывается дважды:
- Один раз для начальной вершины
- Один раз для конечной вершины
- Следовательно, общая сумма степеней равна удвоенному числу рёбер
Следствия из теоремы
| Следствие | Пояснение |
| Чётность суммы степеней | Сумма степеней всегда чётна |
| Количество вершин нечётной степени | В любом графе их число чётно |
Пример расчёта
Рассмотрим граф с 4 вершинами и 5 рёбрами:
- Вершина A: степень 3
- Вершина B: степень 2
- Вершина C: степень 3
- Вершина D: степень 2
Сумма степеней: 3 + 2 + 3 + 2 = 10
Удвоенное число рёбер: 2 × 5 = 10
Применение в теории графов
- Проверка корректности задания графа
- Анализ сетевых структур
- Решение задач о существовании графа с заданными степенями вершин